单摆锤强化学习实例

环境准备

gym                 0.26.2
gym-notices         0.0.8
pygame              2.1.0
torch               1.9.0+cu111

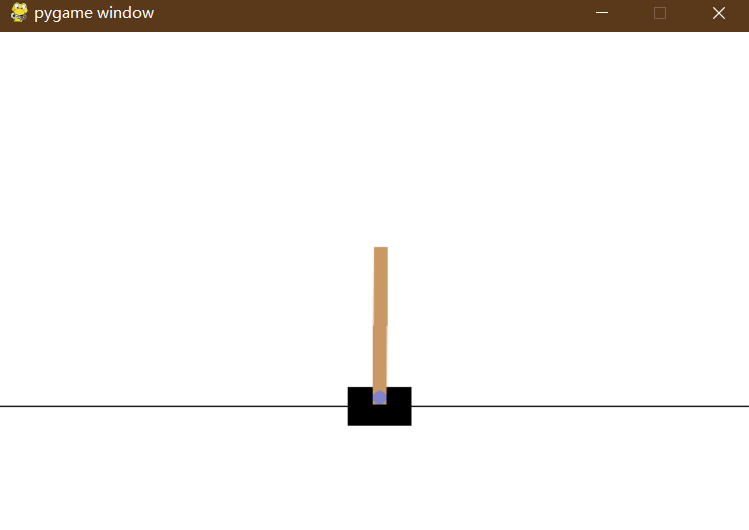
游戏搭建与测试

测试游戏使用的是 gym 库的CartPole-v1 游戏模型。

首先要对游戏环境进行初始化和启动：

# 初始化pygame
pygame.init()
# 生成环境
env = gym.make('CartPole-v1', render_mode='human')

然后，是人类玩家通过键盘来玩游戏，测试和了解游戏的规则以及难度。

# 人类
def human_play(action_max):
    # 游戏初始化
    time.sleep(1)
    print("游戏开始！")
    state, _ = env.reset()
    start_time = time.time()  # 设定游戏开始时间
    step = 0
    fail = False

    # 小车的信息参数
    car_position = state[0] # 小车位置
    car_speed = state[1]    # 小车速度
    pole_angle = state[2]   # 杆子的角度
    pole_speed = state[3]   # 杆子的尖端速度

    for step in range(1, action_max + 1):
        # 渲染画面
        env.render()

        time.sleep(0.2)
        # 以非阻塞方式获取键盘的输入值
        key = pygame.key.get_pressed()
        action = 0

        # 如果键盘没有输入，那么游戏也继续执行下去，输入值将随机选择
        if not key[pygame.K_LEFT] and not key[pygame.K_RIGHT]:
            action = env.action_space.sample()

        # 键盘左箭头为0，右箭头为1
        if key[pygame.K_LEFT]:
            action = 0
        elif key[pygame.K_RIGHT]:
            action = 1

        # agent与环境进行一步交互
        state, _, terminated, _, _ = env.step(action)
        # print('state = {0}:.2f; reward = {1}'.format(state, reward))
        print(f"步骤={step} 行为={action}"
              f" 车速={car_speed:.2f} 位置={car_position:.2f}"
              f" 角度={pole_angle:.2f} 尖端速度={pole_speed:.2f}")

        # 判断当前episode 是否完成
        if terminated:
            fail = True
            print('Done!')
            break

    # 游戏结束后，计算游戏时间和步骤总数
    end_time = time.time()
    game_time = end_time - start_time
    if fail:
        print(f"游戏失败！你坚持了 {game_time:.2f} 秒 {step} 步。")
    else:
        print(f"游戏通关！你坚持了 {game_time:.2f} 秒 {step} 步。")

游戏结果如下：

步骤=1 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=2 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=3 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=4 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=5 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=6 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=7 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=8 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=9 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=10 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=11 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=12 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=13 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=14 行为=1 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=15 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
步骤=16 行为=0 车速=0.03 位置=-0.04 角度=-0.01 尖端速度=-0.03
Done!
游戏失败！你坚持了 3.63 秒 16 步。

于是，定义一个简易的神经网络来玩游戏。

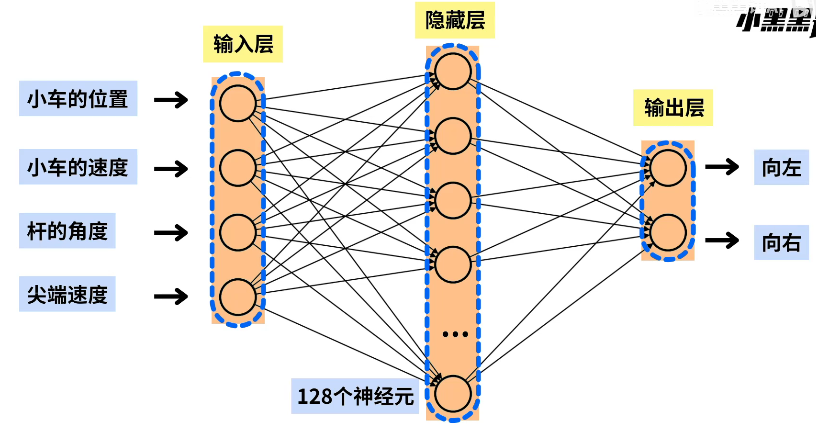
强化学习模型

神经网络

定义的神经网络如上图，输入小车的四个实时特征，输入一个 128 神经元的隐藏层神经网络，最后再输出为向左、向右的概率大小，让神经网络决定小车的向左/向右。

# 神经网络
class CartPolePolicy(nn.Module):
    def __init__(self):
        super(CartPolePolicy, self).__init__()
        # 定义两个线性层，大小分别是4*128与128*2
        self.fc1 = nn.Linear(in_features=4, out_features=128)
        self.fc2 = nn.Linear(in_features=128, out_features=2)
        # 定义一个dropout层，丢弃比率是60%
        self.drop = nn.Dropout(p=0.6)

    # 前向传播函数，输入X
    def forward(self, x):
        x = self.fc1(x)
        x = self.drop(x)
        # 隐藏层的激活函数；在输入数据通过线性层后，ReLU激活函数将其转换为非线性形式，供下一层使用。
        x = F.relu(x)
        x = self.fc2(x)

        # 使用softmax决策最终的行动，决定是向左还是向右
        return F.softmax(x, dim=1)

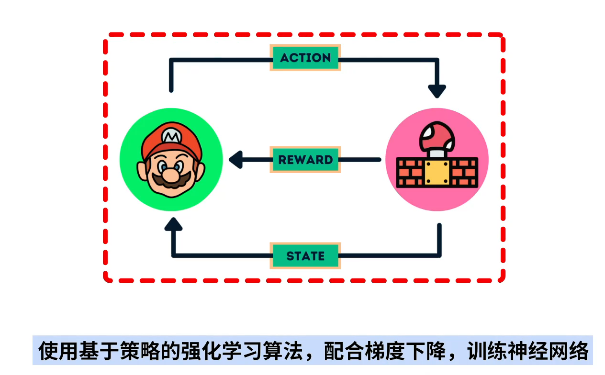
强化学习算法

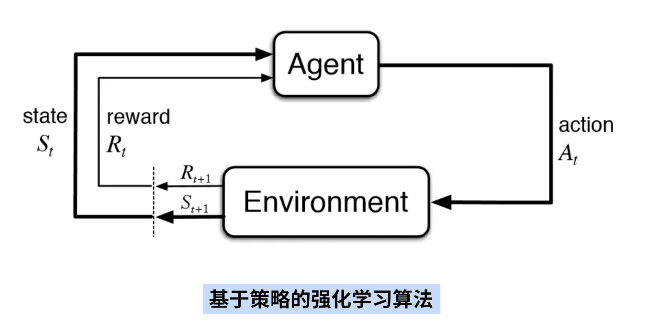
基于策略的强化学习模型其算法而结构如下：

在此处，我们假设 Cartpole 游戏执行了 n 步：

神经网络的行动：$ a1,a2,…….an\in0、1 $

选择动作的概率：$ p1,p2,……pn
$

动作对应的奖励：$ r1,r2,……rn $

总奖励为：$ R=p1r1+p2r2+……+pn*rn $

于是，我们神经网络的参数优化目标为：总奖励 R 最大。

也就是说，增加神经网络输出高奖励动作的概率，减少输出低奖励动作的概率。

问题就在于：如何分配奖励？

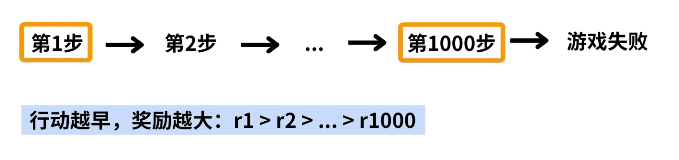
奖励策略

对于 Cartpole 游戏而言：

如果游戏没有结束 ——>正奖励

如果游戏结束 ——>不再奖励

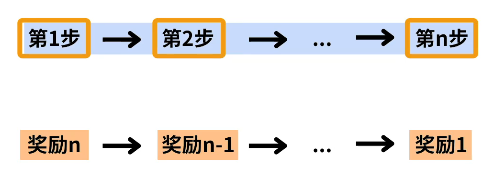
由于第 1 步做出了正确的决定，才有了第 2 步，所以应该给第一步更多的奖励。

所设定奖励策略如下：

损失函数

定义损失函数为：$ loss=-\sum_{i=1}^{n} log(p_i)\cdot r_i $

第 i 步的行动为：$ p_i = \pi(a_i|s_i) $

第 i 步的奖励为：$ r_i=n-i+1 $

神经网络的训练目标即为：使 loss 函数最小的参数模型，即使总奖励 R 最大，

# 实现损失函数的计算方法，函数传入步数n和这n步对应的概率log_p
def compute_policy_loss(n, log_p):
    r = list()
    # 构造奖励列表r
    for i in range(n, 0, -1):
        r.append(i * 1.0)
    r = torch.tensor(r)
    r = (r - r.mean()) / r.std()  # 进行标准化处理
    loss = 0
    # 计算损失函数
    for pi, ri in zip(log_p, r):
        loss += -pi * ri
    return loss

进行训练

# 训练的函数
def train():
    env.reset(seed=543)
    torch.manual_seed(543)

    # 定义模型
    policy = CartPolePolicy()
    optimizer = optim.Adam(policy.parameters(), lr = 0.01)
    '''
    一共训练最多1000回合
    每回合罪多行动10000次
    当某一回合的游戏步数超过5000，就认为训练完成
    '''
    max_episode = 1000
    max_actions = 10000
    max_steps = 5000

    for episode in range(1, max_episode + 1):
        # 对于每一轮循环，都要重新启动一次游戏
        state, _ = env.reset()
        step = 0
        log_p = list()
        
        for step in range(1, max_actions + 1):
            state = torch.from_numpy(state).float().unsqueeze(0)
            # print(state)
            probs = policy(state) # 计算神经网络给出的行动概率

            # 基于网络给出的概率分布，随机选择行动
            m = Categorical(probs)
            action = m.sample()
            '''
            这里不是直接使用概率较大的行动，而是通过概率分布生成action，
            这样可以进一步探索低概率的行动。
            '''
            # agent与环境进行一步交互
            state, _, done, _, _ = env.step(action.item())
            if done:
                break
            log_p.append(m.log_prob(action)) # 保存每次行动对应的概率分布

        if step > max_steps:
            print(f"完成！上一轮训练为{episode}，步数为{step}")
            break

        # 每一回合游戏，都会做一次梯度下降算法
        optimizer.zero_grad()
        loss = compute_policy_loss(step, log_p)
        loss.backward()
        optimizer.step()
        if episode %10 == 0:
            print(f'Episode{episode} Run steps{step}')

    # 保存模型
    torch.save(policy.state_dict(), f'catpole_policy.pth')

AI 测试

接下来让训练生成的模型去玩游戏

def ai_play(action_max):
    # 游戏初始化
    time.sleep(1)
    print("游戏开始！")

    state, _ = env.reset()
    start_time = time.time()  # 设定游戏开始时间
    step = 0
    fail = False

    # 小车的信息参数
    car_position = state[0]  # 小车位置
    car_speed = state[1]  # 小车速度
    pole_angle = state[2]  # 杆子的角度
    pole_speed = state[3]  # 杆子的尖端速度

    # 在环境中，创建神经网络
    policy = CartPolePolicy()
    # 由于网络还有训练，将读取模型的代码load_state_dict注释
    policy.load_state_dict(torch.load('catpole_policy.pth'))
    policy.eval() # 将模型设置为评估模式

    for step in range(1, action_max + 1):
        # 渲染画面
        env.render()

        time.sleep(0.1)

        '''小车控制的方式'''
        # 将环境参数state转化为张量
        state = torch.from_numpy(state).float().unsqueeze(0)
        # 输入至模型policy，计算行动概率probs
        probs = policy(state)

        action = torch.argmax(probs, dim=1).item()

        # agent与环境进行一步交互
        state, _, done, _, _ = env.step(action)
        # print('state = {0}:.2f; reward = {1}'.format(state, reward))
        print(f"步骤={step} 行为={action}"
              f" 车速={car_speed:.2f} 位置={car_position:.2f}"
              f" 角度={pole_angle:.2f} 尖端速度={pole_speed:.2f}")

        # 判断当前episode 是否完成
        if done:
            fail = True
            print('Done!')
            break

        # 游戏结束后，计算游戏时间和步骤总数
    end_time = time.time()
    game_time = end_time - start_time
    if fail:
        print(f"游戏失败！你坚持了 {game_time:.2f} 秒 {step} 步。")
    else:
        print(f"游戏通关！你坚持了 {game_time:.2f} 秒 {step} 步。")

测试结果：

步骤=995 行为=0 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
步骤=996 行为=1 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
步骤=997 行为=1 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
步骤=998 行为=0 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
步骤=999 行为=0 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
步骤=1000 行为=1 车速=0.02 位置=-0.03 角度=0.01 尖端速度=-0.03
游戏通关！你坚持了 42.00 秒 1000 步。

截取部分结果，可见 AI 成功的完成了 1000 步，说明模型很成功。